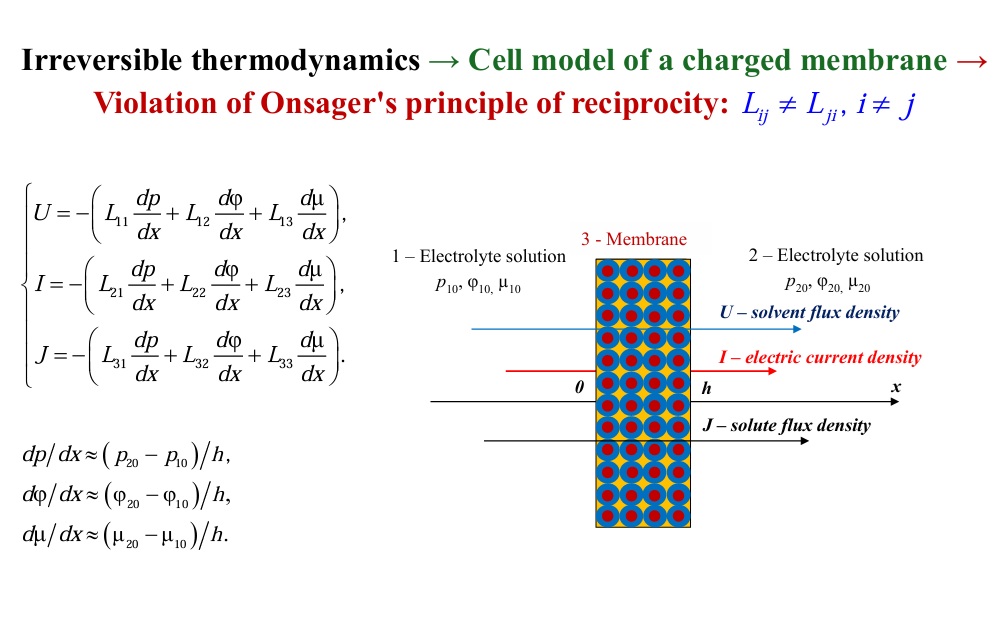
Theoretical study was performed earlier for the cell model of a charged porous membrane based on Onsager’s approach and the result was calculation of all electrokinetic coefficients. Experimental dependences of electroosmotic permeability, conductivity, and diffusion permeability of some perfluorinated membranes on electrolyte concentration were simultaneously and quantitatively described using exact analytical formulae based on the same set of physicochemical and geometrical parameters. It is shown here that for the developed cell model of the ion–exchange membrane, the Onsager principle of reciprocity is violated—the coupled cross kinetic coefficients are not equal. The violation is associated with the fact that the reciprocity principle takes place only for systems for which generalized fluxes are zero at thermodynamic forces other than zero within the framework of linear thermodynamics of irreversible processes.

The paper reflects on the author’s experience of teaching mathematics education courses to teacher candidates using technology. It demonstrates both explicit and hidden presence of asymmetry among the topics included in the courses and shows what it brings to the study of mathematics for teaching by future teachers of the subject matter. Examples associated with asymmetry deal with pizza sharing, an irrational inequality, a quadratic equation with parameters the loci of which exhibit asymmetry, and asymmetrical modification of Pascal’s triangle leading to Fibonacci-like polynomials the roots of which alternate symmetrical and asymmetrical location within a certain interval on the number line. The examples presented in the paper are supported by digital tools including dynamic geometry programs, Wolfram Alpha, Maple, a spreadsheet and the graphics of Microsoft Word. The paper argues for the importance of the modern-day computational tools in revealing conceptually rich structure of mathematics, including the interplay between symmetry and asymmetry, to future K-12 teachers of the subject matter. Several reflective comments of the teachers on their learning experiences to teach mathematics conceptually in the technological paradigm are shared and analyzed.

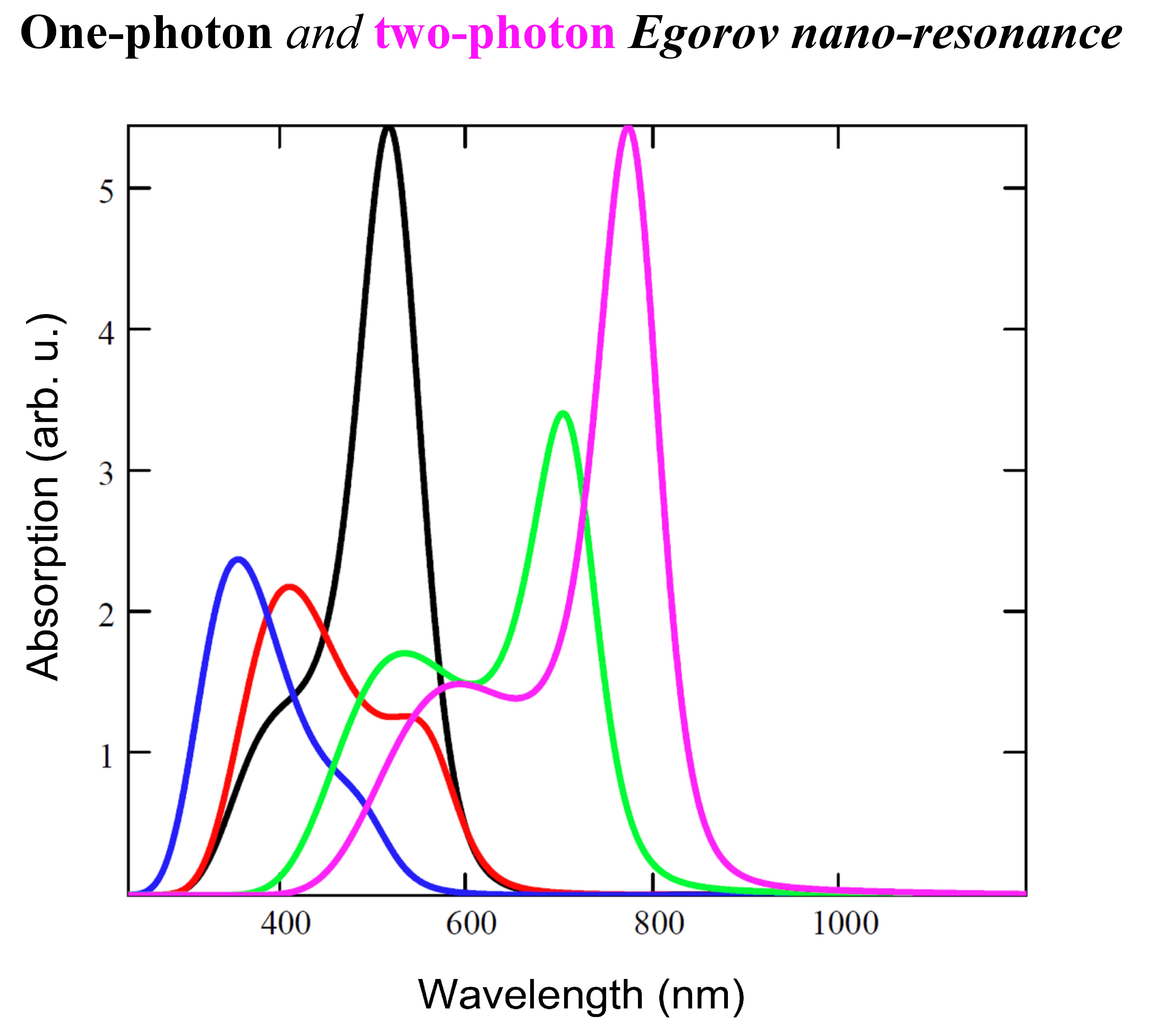
A new theoretical approach is proposed to explain the nature of the well-known narrow and intense optical J-band of J-aggregates of polymethine dyes. The old approach proposed by Franck and Teller in 1938 and based on the Frenkel exciton theory does not take into account the specific properties of the main optical chromophore of polymethine dye monomers—the polymethine chain. In the new approach proposed by Egorov and based on a new fundamental physical theory—quantum‒classical mechanics, which takes into account the chaotic and regular dynamics of the transient state, the optical properties of the polymethine chain and monomers as a whole are considered as a key factor determining the unique optical properties of J-aggregates. The J-band is explained by the so-called Egorov resonance, the presence of which follows from quantum‒classical mechanics. Many other experimental facts have also been explained on the basis of quantum‒classical mechanics. These include: asymmetry of the shape of the luminescence bands of J-aggregates relative to their optical absorption, an anomalously small Stokes shift of the J-band; the shape of the optical bands of dimers, H- and H*-aggregates; strong detuning of the Egorov resonance during the transition from one-photon to two-photon absorption. The conditions for the restoration of the Egorov resonance during two-photon absorption are predicted.

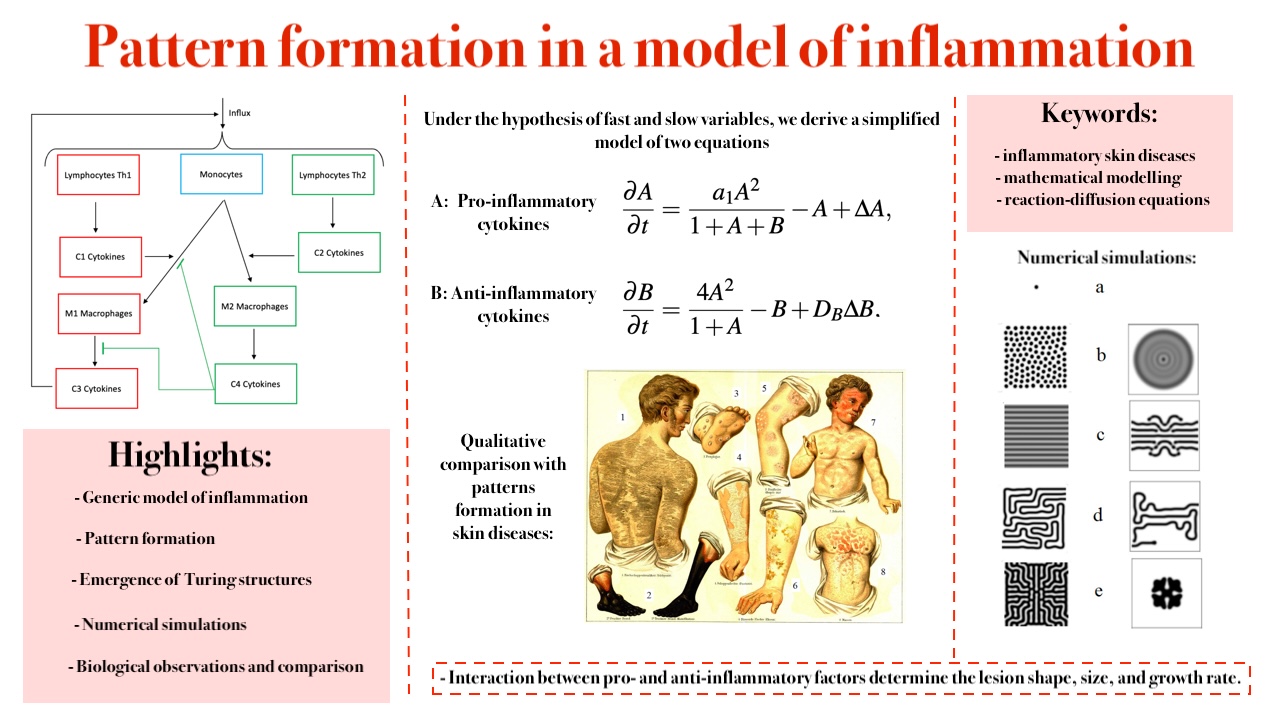
Inflammation is the body's response to infection, injury, or other stimuli. Acute inflammation is a crucial component of the immune system's defense, aimed at eliminating infected or damaged cells and halting disease progression. A subtle interaction between pro- and anti-inflammatory processes determines its progression to inflammation resolution or to chronic inflammation. In this study, we propose a generic model of inflammation through a system of reaction-diffusion equations involving various inflammatory and anti-inflammatory cells and cytokines. We investigate the formation of patterns, determined by the emergence of Turing structures, through linear stability analysis and numerical simulations. These theoretical findings are further supported by observations of similar patterns in skin diseases.

Linking methods are frequently applied to analyze the performance of two groups on a set of items. This article shows analytically and by simulation that the occurrence of differential item functioning (DIF) can induce bias and additional variance in parameter estimates of the linking method. Interestingly, the bias of the parameter estimates of a linking method depends on whether random DIF occurs in one or two groups ( i.e., the type of DIF effects). The findings are shown utilizing asymmetric and symmetric Haebara and Stocking-Lord linking. Moreover, the latter linking methods were compared with recently proposed corresponding SIMEX-based variants of linking in a simulation study. It turned out that SIMEX-based linking provided unbiased estimates of whether the correct assumption of the type of DIF effects has been implemented.

In this article, we propose and study an improved version of the cosine distribution. Its main features are to be with support [-1, 1], to be mainly asymmetric by construction, and to be simple and flexible from a functional point of view, in particular, it retains the cosine feature that allows it to generate oscillatory shapes and multimodes, to unify the cosine distribution and the truncated exponential distribution, and to be used as a statistical model in different scenarios involving data contained in [-1, 1]. We provide the main theory, including an expression of the key functions, quantiles and moments. Numerical work is carried out to determine the main measures of skewness and kurtosis. The practicality of the proposed distribution is illustrated with some data fitting scenarios, supported by graphical analysis.